圆周率是对圆形和球体进行数学分析时不可缺少的一个常数，各国古代科学家均将圆周率作为 一个重要课题。我国最早采用的圆周率数值为3，即所谓“径一周三”。《九章算术》中就采用了这个数据，“方田”中有这样一个问题 “今有圆田，周三十步，径十步，问田有几何?”很显然，这个数值不能满足精确计算的要求。汉代 一些数学家已发现了这 一问题，并在实际应用时采用多种圆周率数值。如刘歆作标准容器“律嘉量斛”时用3.154;张衡在《灵宪》中取用730/232，约等于3.1466，在球体积公式中又采用，约等于3.1623; 三国王蕃采用的数据相当于3.1556。上述这些数值精确度虽有提高，但大多是经验成果，缺少理论基础。

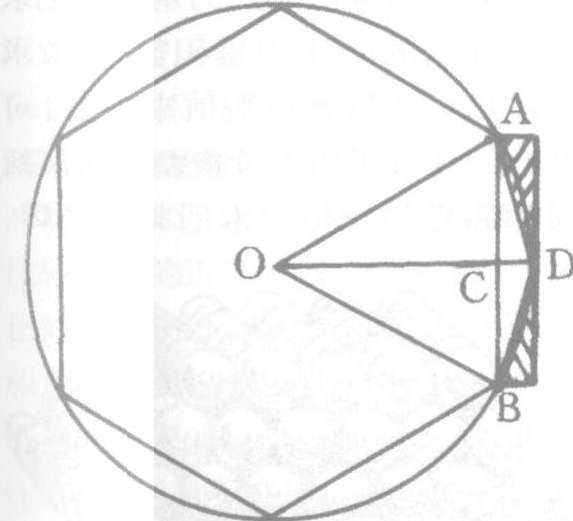
刘徽割圆术示意图

圆周率计算上的有所突破，有赖于有效方法的诞生，这种方法就是割圆术。刘徽在为《九章算术》作注的时候，指出 “周三径一”不是圆周率，而是圆内接正六边形周长和直径之比。经过深入研究，他发现圆内接正多边形边数无限增加时，多边形周长可无限逼近圆周长，从而创立了“割圆术”。割圆术的主要内容是： 一、在圆内作内接正六边形，每边边长均等于半径; 再作正十二边形，从勾股定理出发，求得正十二边形的边长，如此类推，从内接n边形的边长可推知内接2n边形的边长。二、从圆内接正n边形每边边长，可求得内接2n边形的面积。如图正十二边形的 一部分(四边形OADB)的面积，等于正六边形边长AB乘以半径OD的 一半，这样，即使边数极多的内接正多边形面积也可以一步步求解。三、刘徽进一步指出，圆的面积介于两个可求得的值之间。例如，圆面积大于正十二边形面积，但正十二边形的每个部分都加上一个小三角形(图中阴影部分)，总的面积便又大于实际圆面积。显然，阴影部分的面积可由正十二边形与正六边形的面积差求得。这样，刘徽实际上发现，圆面积S满足不等式S_2n<S<S_2n+(S_2n-S_n)，这里S是圆面积，S_2n、S_n是内接正多边形面积，n、2n为边数。

《隋书·律历志》 中有关圆周率的记载

依据极限观念，刘徽指出：随着圆内接正多边形边数的增加，它的周长和面积越来越接近圆周长和圆面积，“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”。将这种极限思想和上述不等式结合起来，通过不断增加多边形边数，就可以从不足近似值和过剩近似值两个方面逼近圆周率的真值。刘徽使用这一方法，从圆内接正六边形算起，相继算出正十二边形、正二十四边形，直至正一百九十二边形边长，并求得正一百九十二边形的面积为3.1464/625，相当于求得π为3.141024。他还继续计算，最后求出正三千零七十二边形的面积，得到π的近似值为3.1416。这两个数据的精确度是当时世界上前所未有的。

与刘徽类似的是，古希腊的阿基米德也用正多边形法去求圆周率，他认为圆周长介于圆内接正多边形边长与外切正多边形边长之间，算得310/71<π<31/7。但是阿基米德是用归谬法证得这 一结果的，他避开了极限概念，而刘徽却大胆地应用了以直代曲、无限趋近的思想方法; 且阿基米德的方法需另外计算圆外切正多边形面积，刘徽的方法则只需求内接正多边形面积。与阿基米德比，刘徽的割圆术可谓事半功倍。

本文地址： https://www.yishiweijian.com/zhonghua/20221230455.html

文章来源：主编

版权声明：除非特别标注，否则均为本站原创文章，转载时请以链接形式注明文章出处。